Une exploitation du photogramme de Jacques Tati lors d’une séance de mathématiques
Norbert Nagy,
Collège Pierre Mendès France, Tourcoing
• Objectif :
L’analyse du photogramme a pour but de permettre de manipuler les notions de grandeurs et de mesures pour déterminer en particulier la largeur d’une allée, telle que l’on peut l’apercevoir sur le document. Ces notions seront donc mises à l’épreuve d’un calcul de probabilité, sans oublier une sensibilisation à la notion de perspective.
La séance a pour but de matérialiser les premières observations faites pendant la séance de français en s’intéressant aux mesures de l’espace représenté pour en accroître encore la rigueur géométrique.
Quelles sont précisément les mesures de cet espace labyrinthique dans lequel l’homme semble se perdre ?
• Déroulé de la séance :
Les élèves savent que les distances sur une carte ou un plan sont proportionnelles aux distances réelles. Peut-on appliquer cette propriété dans cette situation ?
– Sur une carte ou un plan, il y a nécessairement une légende qui apparaît indiquant l’échelle utilisée. Ce n’est pas le cas ici. Sans échelle, on ne peut rien faire. À moins de connaître la taille réelle d’un objet apparaissant sur la photo, alors on pourrait utiliser la proportionnalité et ainsi résoudre le problème.
– Mais peut-on utiliser la proportionnalité dans le cas d’une photo ?
Pour comprendre le problème, j’ai représenté à main levé au tableau deux images sensées représenter la même scène :
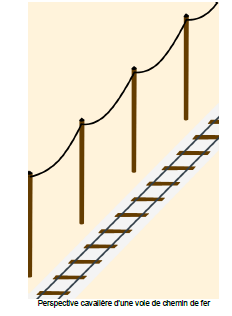
1. Cette image semble-t-elle réaliste ? Pourquoi ?
2. Ne comporte-t-elle pas un défaut de réalisme ? Lequel ?
Pour les élèves, c’est une image réaliste, et ils n’ont pas perçu la différence qu’il y a par rapport à une photo.
Sur ce genre de figure, on peut appliquer la proportionnalité sans problème lorsque l’échelle est connue.
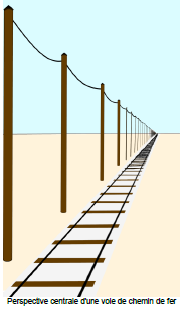
 1. Cette image semble-t-elle réaliste ? Plus ou moins que la précédente ? Pourquoi ?
1. Cette image semble-t-elle réaliste ? Plus ou moins que la précédente ? Pourquoi ?
2. Peut-on y définir une échelle ? Pourquoi ?
Pour les élèves, cette seconde image est plus réaliste que la première, cependant, ils ont du mal à comprendre pourquoi. Il a fallu réfléchir longtemps avant de prendre conscience que plus un objet se trouve au loin, plus il devenait petit.
Le fait que des objets identiques puissent avoir différentes tailles selon leur position dans l’image nous empêche de pouvoir définir une échelle, de sorte qu’a priori, on ne pourra pas utiliser la proportionnalité.
Cependant, si l’on se place dans un plan parallèle au cadre de la photo, le phénomène de différence de taille avec l’éloignement sera moins marqué : sur l’extrait suivant, les distances 1, 2 et 3 sont différentes car plus on se trouve à droite de l’objectif, plus on s’en éloigne, cependant la différence reste minime. On pourra donc évaluer des distances dans ce plan à condition de prendre les mesures sans trop s’éloigner de l’élément dont on veut avoir la mesure et surtout en gardant en tête que l’on obtiendra une valeur approximative.
Ce sont donc les valeurs 1 ou 2 qui vont nous servir par la suite.
Nous aurions pu essayer d’utiliser la taille des individus pour résoudre le problème. Mais cela pose davantage de problème du fait de leur positionnement par rapport aux cloisons. De plus, la partie située au niveau du sol est peu visible sur le document utilisé pour prendre les mesures (photocopie), les pieds des individus et des cloisons sont invisibles du fait de couleurs sombres complètement bouchées. La vue plongeante est en outre un facteur à fausser les évaluations de distance.
On constate que les cloisons semblent être formées de quatre panneaux identiques dont l’un sert de porte. Ceci devrait nous permettre de faire avancer le problème car il faut normalement respecter des standards dans les constructions, et la largeur des portes en fait partie.
Les élèves ont eu donc comme consigne de faire une recherche sur la largeur standard d’une porte (d’intérieur).
Comme on ne savait pas à ce moment où se situait la scène, j’ai demandé d’élargir la recherche à l’Angleterre et aux États-Unis pour interroger la notion de normes et de standards.
Ensuite j’ai fait remarqué que les automobiles visibles à l’arrière plan étaient visiblement d’une autre époque. Il fallait donc encore élargir la recherche aux années 60. Il s’en est suivi une discussion sur l’utilité des standards. Sur leur évolution (prise en compte des chaises roulantes pour handicapés).
Les recherches permettent de retrouver les normes en vigueur, en revanche, aucune information sur les normes en vigueur pendant les années 60.
Nous avons donc décidé dans un premier temps d’effectuer les calculs pour différentes valeurs de largeur de portes :
60 cm, 70 cm, 80 cm, et 90 cm. Nous avons alors obtenu 4 propositions pour la largeur de l’allée. Il ne restait plus qu’à choisir celle qui était la plus crédible.
Nous avons donc décidé dans un premier temps d’effectuer les calculs pour différentes valeurs de largeur de portes :
60 cm, 70 cm, 80 cm, et 90 cm. Nous avons alors obtenu 4 propositions pour la largeur de l’allée. Il ne restait plus qu’à choisir celle qui était la plus crédible.
Nous nous sommes intéressés aux deux personnes situées au fond de la salle. Du fait de l’éloignement, l’effet de la vue plongeante est moins important. En prenant successivement les valeurs trouvées précédemment, nous avons, toujours en utilisant la proportionnalité, déterminé la hauteur des deux personnages (un homme et une femme). Étant donné qu’une hauteur de 1,65 m semblait être la plus probable, nous en avons déduit que la largeur d’une cloison devait être d’environ 70 cm.

Nous avons donc décidé dans un premier temps d’effectuer les calculs pour différentes valeurs de largeur de portes :
60 cm, 70 cm, 80 cm, et 90 cm. Nous avons alors obtenu 4 propositions pour la largeur de l’allée. Il ne restait plus qu’à choisir celle qui était la plus crédible.
Nous nous sommes intéressés aux deux personnes situées au fond de la salle. Du fait de l’éloignement, l’effet de la vue plongeante est moins important. En prenant successivement les valeurs trouvées précédemment, nous avons, toujours en utilisant la proportionnalité, déterminé la hauteur des deux personnages (un homme et une femme). Étant donné qu’une hauteur de 1,65 m semblait être la plus probable, nous en avons déduit que la largeur d’une cloison devait être d’environ 70 cm.
Bien sûr, les mesures prises sur la photocopie étant faites au millimètre près, nous en avons profité pour évaluer la marge d’erreur que cela représente sur le résultat final, soit environ une dizaine de centimètres.
Les élèves ont donc été capables d’établir les mesures de l’espace représenté, un espace fait de normes, de règles, un nouveau monde de « l’Identique ».


